ボリンジャーバンドとはどういうインジケーターなのか、どのような計算式で成り立っているものなのか、を調べていくと、必ず以下のような計算式に行き着きます。
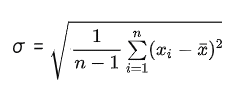
そして、この計算式が「標準偏差」と呼ばれるものの計算式である事が分かり、
| ボリンジャーバンドとは標準偏差に基づく値を表示しているインジケーターである |
という事を知るわけですが、この「標準偏差」というものが何なのか、どのような理論の上で算出されている値なのか、といったところまでは、あまり認知されていないのが実情だと思います。
実際にボリンジャーバンドをテクニカル分析に用いているトレーダーも含めて、そこをあまりよく分からないまま漠然と利用しているトレーダーが非常に多いという事です。
ただ、自分自身が利用しているインジケーターの計算式の「成り立ち」や「理論」を理解していないような状況は『その指標に基づく売買の合理性や理由を理論的に説明できない状況』と変わりません。
自分自身が何をアテにして、どのような理論に基づいて売買を行っているのかを自分自身が「分かっていないに等しい」という事です。
そこで本講座では、実際に利用しているトレーダーも多い「ボリンジャーバンド」において、
| ・その計算式によって求めている『標準偏差』とは、どのような値なのか。 ・その『標準偏差』の計算式はどのような理屈、理論の上で成り立っているのか |
などを順を追って詳しく解説していきたいと思います。
ボリンジャーバンドにおける「標準偏差」とは何なのか。
先ほど示した「ボリンジャーバンド(標準偏差)の計算式」は、一定期間のデータ(レート)のばらつき(散らばり)を数値化するための数式であり、厳密には以下の「2つの計算式」から成り立っています。
| 平均値に対して「ばらつき」があるデータの差(「偏差」の値)を求める計算式 |
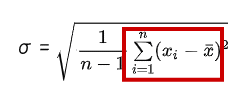
| 「偏差」を二乗した値の平均(「分散」の値)を求める計算式 |
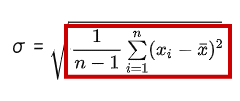
上記の計算式を経て算出した『分散』と呼ばれる値の「平方根(√)」が『標準偏差』にあたります。
「∑(シグマ)」記号の意味この手の数式で出て来る「∑(シグマ)」は、上記の数式で言えば「i」を「1」から「n」まで順に変化させ,そのすべてを足し合わせなさい、という意味合いになります。 |
この『分散』や『標準偏差』は、統計学における「データのちらばりを数値化するための公式」であり、この数値化には『偏差』と呼ばれる値がその「元」となっているわけです。
この『偏差』の考え方は、データのばらつきを『平均値に対する偏り(乖離)』とした上で、
| 1:平均の値を求める(計算する) 2:平均の値と個々のデータの差を求める |
このようなプロセスによって求められる数値が『偏差(平均値に対して「ばらつき」があるデータの差)』であり、ボリンジャーバンドで言えば、これを以下のような計算で求めています。
↓↓↓
| 1本1本のローソク足の終値 - 一定期間の終値平均 = 偏差(終値平均との乖離) |
このような計算によって、終値平均の算出対象となったローソク足1本1本の終値における「偏差(終値平均との乖離)の値」が求められているわけです。
▼「偏差」の算出事例例えば、以下のような値動きとなっている相場があった場合、
このような相場の1つ1つのデータ(終値)の「偏差」の値は、 ・平均レート:(100 + 105 + 110 / 3) = 105円(3日間の平均レート) このようになるという事です。 |
一定期間の終値平均に対する個々の終値の乖離 = 偏差
このような『偏差』の値を求めていく計算式が、ボリンジャーバンド(標準偏差)の計算式内の以下の計算式にあたります。
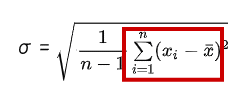
ただ『偏差』の値は「個々のデータ(終値)のばらつきを示す値」のため、一定期間の相場内でどれくらいの終値のばらつきがあったのかを数値化するには、個々の『偏差』の値を1つにしなければなりません。
そこで以下のような「個々の偏差を二乗した値を平均(※データ数-1の平均)する計算式」によって、データのばらつきの指針となる『分散』という値を算出する事ができます。
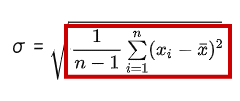
この計算式によって、個々のローソク足の終値から求めた『偏差』の値から、その「ばらつき」の指針となる『分散』の値を求めているという事です。
▼「分散」の計算式の意味と算出事例この「分散の公式」においては、
といった疑問が当然、生じるところかと思いますが『分散』の値を求める際の『偏差』の値は「平均値との差」という特性上、これらの合計値は以下のように必ず「0」になってしまいます。 偏差の合計:(+5)+(-5) = 0
といった考え方があり
この2つの計算式は、それぞれの以下のように異なるものになっています。 「標本の標準偏差を求める場合の計算式」 「母集団の標準偏差を求める場合の計算式」 上記の通り、標本の標準偏差を求める場合は「n-1」で偏差の平均を計算しますが、母集団の標準偏差を求める場合には「n-1」ではなく「n」で偏差の平均を計算します。 *** よって、先ほどと同じ例で「分散」を求めた場合には、
このような相場の1つ1つのデータ(終値)の「偏差」の値は、 分散:(5の二乗 + -5の二乗)/ (3-1) = 12.5 |
一定期間の終値平均に個々の終値のばらつきの指針 = 分散
ただ、ここまでの計算式で求めた『分散』の値は、算出の際に個々のデータ1つ1つを「二乗」している関係から、この『分散』の値をそのまま「平均」の値などの対比に用いる事はできません。
そこで、二乗された単位(数値)を元に戻すために『分散』の平方根(√)を求める計算を行っているのが、以下の『標準偏差』の計算式に他なりません。
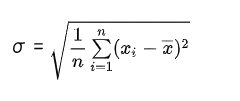
つまり、このボリンジャーバンド(標準偏差)の計算式は『偏差』の値から『分散』の値を求め、その平方根(√)を求めたもの、という事です。
よって、このような計算式に基づいた「標準偏差」は、その値が大きいほど「その対象となった期間の終値が大きくばらついている事」を意味します。
その上で、ボリンジャーバンドの基本的な考え方は、
| ・ばらつきが大きい相場が続くほど現在レートが平均レートに対して乖離する可能性も高くなる ・ばらつきが小きい相場が続くほど現在レートが平均レートに対して乖離する可能性は低くなる |
このような前提において、現在レートが平均レートに対して乖離する「想定範囲」を標準偏差の値に基づく形で示しているのがボリンジャーバンドというインジケーターに他ならないという事です。
***
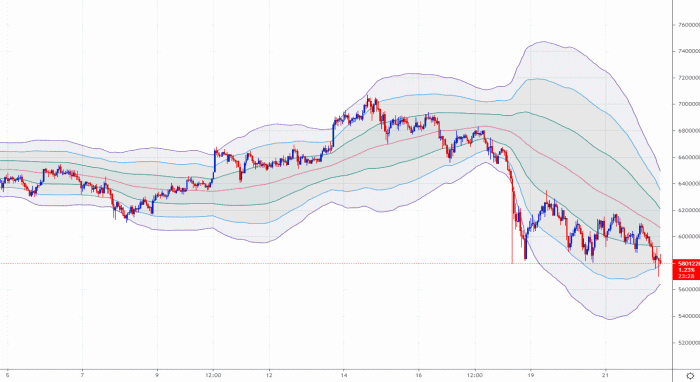
その上で、ボリンジャーバンドにおいては、以下の「確率」が併せて提示されている傾向にあります。
| ±1σの範囲内(※下記、緑色のバンド内)で相場が動く確率:68.27% ±2σの範囲内(※下記、青色のバンド内)で相場が動く確率:95.45% ±3σの範囲内(※下記、紫色のバンド内)で相場が動く確率:99.73% |
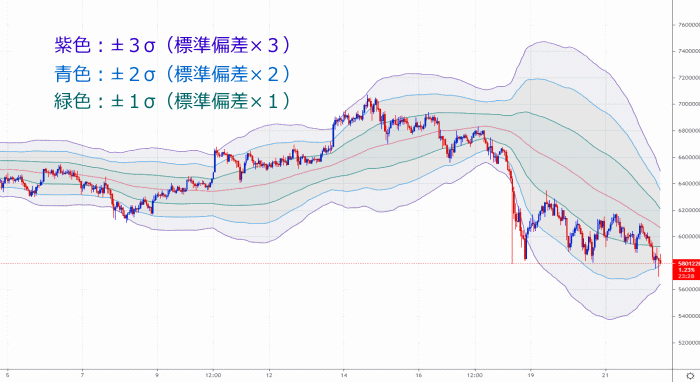
ただ、上記の「確率」は実際の相場の値動きを統計した裏付けのある数字ではないため、実際の相場の「終値」は全くもって、上記のような確率の範囲には納まらないのが実情です。
ボリンジャーバンドの±3σ(画像内、紫色の外側のバンド)の範囲内に、相場が99.7%の確率で納まるというような情報や認識は「事実とは異なる(間違っている)」という事です。
そんな「ボリンジャーバンドにおける誤った認識」や「事実と異なる確率論」については、以下の記事で詳しく解説していますので、こちらも併せて是非、参考にしてください。
↓↓↓
以上、本講義ではボリンジャーバンドの計算式の意味(意図)や、その計算式によって求めている「標準偏差」について解説させて頂きました。
今回のテーマに関連する講義が幾つかございますので、こちらも是非、参考にして頂ければと思います。
|
>テクニカル指標の優劣~有効性の高いインジケーターの考察~ |
本講義の内容が、少しでも今後のあなたの資産運用のお力添えになれば幸いです。
最後までお付き合い頂き、ありがとうございました。
